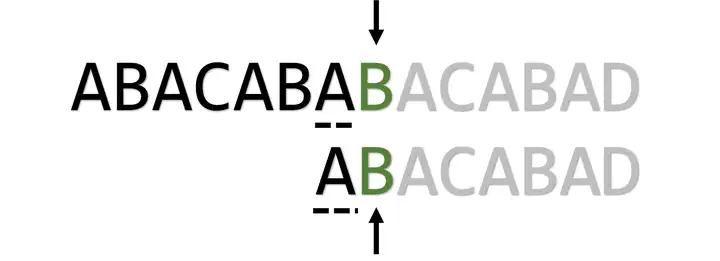【算法】KMP算法

引子

KMP算法，也叫做Knuth-Morris-Pratt算法，是常见的字符串匹配算法，效率很高，能在$O(n)$复杂度内求解字符串匹配问题。

我自己用C语言大概写过三四回KMP算法，每次都有大大小小的bug。这次我就来好好捋一捋KMP算法的原理。

暴力匹配算法

伪代码如下：

int TrivialMatch(string pattern, string text) {
    int pattern_len = pattern.length;
    int text_len = text.length;
    for (int text_p = 0; text_p <= text_len - pattern_len; text_p++) {
        for (int pattern_p = 0; pattern_p < pattern_len; pattern_p++) {
            // Check one by one
            if (pattern[pattern_p] != text[text_p + pattern_p])
                break;
        }
        // If all matched
        if (pattern_p == pattern_len) return text_p;
    }
    return -1;
}

该方法时间复杂度为$O(mn)$，其中$m,n$分别为文本和模式子串的长度。

用动画(来自https://segmentfault.com/a/1190000022642180)表示出来就是这样的：

简短的分析

该方法的缺点是，不论在文本串还是模式子串上，二者的指针都会回退，有没有什么方法不让指针回退呢？

匹配失败的时候，模式子串的指针必须回退，那么可不可以让文本串的指针不回退，尽可能少地回退模式串的指针呢？KMP算法便是应用这种思想的一种算法。

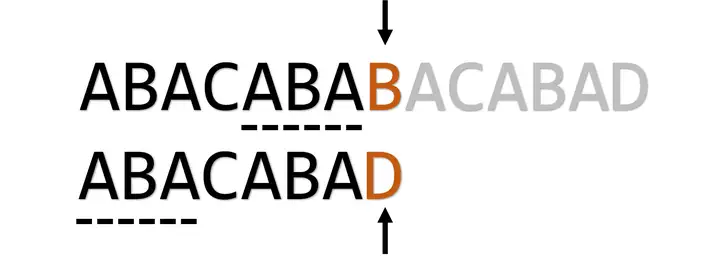
具体怎么应用？试想一下，进行如下的匹配时：

B和D不匹配，但是我们知道前面的ABACABA已经匹配上了，而且其具有最长的、相等的前缀后缀ABA。如何最小程度回退模式串的指针？我们可以让模式串的指针回退到C，因为只有回退到C，才能保证模式串指针之前的部分和文本串匹配：

应用如上原理：

OK，如何实现？

KMP算法: next数组的计算

next数组，就是用来记录模式子串的、每个位置对应的最长前缀后缀的数组。

C++实现:

vector<int> CalculateNext(string pattern) {
  vector<int> next {0};
  int prefix_length = 0;
  int pointer_pattern = 1;
    
  while(pointer_pattern < pattern.size()) {
    if(pattern[pointer_pattern] == pattern[prefix_length]) {
      next.push_back(++prefix_length);
      pointer_pattern++;
    } else {
      if(prefix_length == 0) {
	next.push_back(0);
	pointer_pattern++;
      } else {
	prefix_length = next[prefix_length - 1];
      }
    }
  }
    
  return next;
}

设立两个变量，一个用来记录当前最长的前缀长，一个用来遍历模式子串。若二者对应的字符相等，则二者都加一，并让此时的next数组值为最长的前缀长；若不相等，当最长前缀长为0，说明第一个字符和此时的字符不等，直接让next数组值为0，否则，让最长前缀长等于前一个字符的最长前缀长，由于长度和索引的不等关系，该方法能合理的移动标尺——Quite hard to understand.

可以手动推一推。

KMP算法： 匹配过程

C++实现如下：

bool KMP(string text, string pattern) {
  vector<int> next = CalculateNext(pattern);
  int pointer_pattern = 0, pointer_text = 0;
  while((text.size() - pointer_text) >= (pattern.size() - pointer_pattern)){
    if(pattern[pointer_pattern] == text[pointer_text]) {
      pointer_pattern++;
      pointer_text++;
    }
    if(pointer_pattern == pattern.size()) {
      return true;
    } else if(pointer_text < text.size() && pattern[pointer_pattern] != text[pointer_text]) {
      if(pointer_pattern != 0) {
	pointer_pattern = next[pointer_pattern - 1];
      } else {
	pointer_text++;
      }
    }
    
  }
  return false;
}

这算是一种比较繁琐，但是比较清晰的实现方法。先计算模式串的next数组，然后匹配，while里的条件是判断文本串剩下的长度是否不少于模式串剩下的长度，防止可能出现的溢出。接着，就按照上面提到的方法实现即可。

实战

本题为洛谷P3375:【模板】KMP 字符串匹配:

#include <iostream>
#include <vector>
#include <string>

using namespace std;

vector<int> CalculateNext(string pattern) {
    int prefix_length = 0, pattern_p = 1;
    vector<int> next;
    next.push_back(0);
    while(pattern_p < pattern.size()) {
        if(pattern[pattern_p] == pattern[prefix_length]) {
            next.push_back(++prefix_length);
            pattern_p++;
        } else {
            if(prefix_length == 0) {
                next.push_back(0);
                pattern_p++;
            } else {
                prefix_length = next[prefix_length - 1];
            }
        }
    }
    return next;
}



int main(int agrc, char **argv) {
    string text, pattern;
    cin >> text >> pattern;
    vector<int> next = CalculateNext(pattern);
    int text_p = 0, pattern_p = 0;
    while(text_p < text.size()) {
        if(text[text_p] == pattern[pattern_p]) {
            text_p++;
            pattern_p++;
        }
        if(pattern_p == pattern.size()) {
            cout << text_p - pattern_p + 1<< endl;
            pattern_p = next[pattern_p - 1];
        } else if(text_p < text.size() && text[text_p] != pattern[pattern_p]) {
            if(pattern_p == 0) {
                text_p++;    
            } else {
                pattern_p = next[pattern_p - 1];
            }
        }
    }
    
    for(int border : next) {
        cout << border << " ";
    }
    return 0;
}